十大排序算法(经典)

分类

• 交换类
  • 冒泡排序
  • 快速排序
• 分配类
  • 计数排序
  • 基数排序
• 选择类
  • 选择排序
  • 堆排序
• 归并类
  • 归并排序
• 插入类
  • 插入排序
  • 希尔排序

(一)冒泡排序

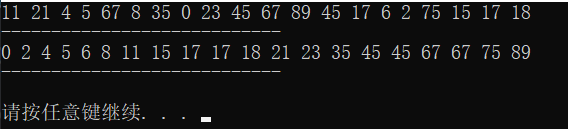
这是一种基于交换的排序，这里用升序举例，若后一个数比当前的数小则交换两者数值，以此进行到
末尾两个数为止。这样最大的数就被排到了最后一位，下一轮又把第二大的数排到倒数第二位，依此类推。
最终我们一共要冒泡n次，每次冒泡循环n-1次
下面是基础的冒泡排序:

#include <stdio.h>
#include <time.h>
#define MAXSIZE 20

void showArr(int arr[],int length)   //打印数组
{
    for (int i = 0; i < length; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n----------------------------\n");
}
void sortArr(int arr[],int length)
{
    while (length-- && flag)
    {
        for (int i = 0; i < length; i++)
        {
            if (arr[i+1]<arr[i])
            {
                int temp=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=temp;
            }
        } 
    }
}
int main()
{
    int arr[MAXSIZE]={11,21,4,5,67,8,35,0,23,45,67,89,45,17,6,2,75,15,17,18};
    showArr(arr,MAXSIZE);    //初始序列
    sortArr(arr,MAXSIZE);
    showArr(arr,MAXSIZE);    //排序后序列
    return 0;
}
//这是基础版的冒泡排序

考虑上面的排序机制，可以发现，每一次都会进行完整的冒泡，这样不管原本的序列混乱度如何，每次都会把程序执行完。因此考虑让程序优化。
优化思路:设置flag来检测当前序列是否已经达到完全有序状态，若达到，这不在，不在继续循环。若未依旧没有排好序则继续执行程序。
运行结果：

//其它地方都一样，我们只改变排序函数sortArr
void sortArr(int arr[],int length)
{
    int flag=1;
    //flag为1则进入循环表示当前数组不是完全有序的
    while (length-- && flag)
    {
         flag=0;
         //把flag置0
        for (int i = 0; i < length; i++)
        {
            if (arr[i+1]<arr[i])
            {
                flag=1;
                //出现了非有序关系。所仪改变flag为1
                int temp=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=temp;
            }
        } 
    }
}
//这是优化过的冒泡排序，筛选掉了后期的无效排序

运行结果:

我们看到结果一致，但比较两种机制，显然优化后的程序效率有略微提升。

(二)选择排序

这是基于冒泡排序的的改进，在每一轮比较中选出最小的放到最前面，
以此进行n-1轮，因为最后一轮只有一个数，所以不用在进行交换。
下面是选择排序的函数:

void seclectArr(int arr[],int length)
{
    for (int i = 0; i < length; i++)
    {
        int k=i;
        for(int j=i+1;j<length;j++)
           if(arr[j]<arr[k])
             k=j;
        int temp=arr[i];arr[i]=arr[k];arr[k]=temp;
    }
    
}

注：因为在每次排序完成后。数组前面部分已经有序(已经是最小的)，所以内成循环不用从头卡开始，而是从当前位置往后。
主函数中调用后运行结果:

结果依然未变

(三)插入排序

插入排序是专门针对有序度高的序列的排序，思想是通过交换，
在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。对于数量少且有序度高的序列，其效率可观。
插入排序函数:

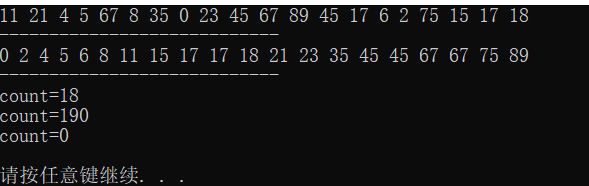
void insertArr(int arr[],int length)
{
    count=0;
    for(int i=1;i<length;i++)
    {
        for(int j=i;j>=1 && arr[j]<arr[j-1];j--)
        {
            count++;
            int temp=arr[j-1];
            arr[j-1]=arr[j];
            arr[j]=temp;
        }
    }
}
int main()
{
    int arr[MAXSIZE]={11,21,4,5,67,8,35,0,23,45,67,89,45,17,6,2,75,15,17,18};
    showArr(arr,MAXSIZE);    //初始序列
    insertArr(arr,MAXSIZE);
    showArr(arr,MAXSIZE);    //排序后序列

    sortArr(arr,MAXSIZE);
    printf("count=%d\n",count);
    seclectArr(arr,MAXSIZE);
    printf("count=%d\n",count);
    insertArr(arr,MAXSIZE);
    printf("count=%d\n",count);
    return 0;
}
//count用于计数循环次数

结果展示:

可以看到，对于有序数组，插入排序效率明显高于冒泡和选择。

(四)希尔排序

优化版的插入排序，原来插入排序的步长是1，希尔排序的步长可以很大，然后逐渐减小到1形成插入排序
(为了更好的验证希尔排序的稳定性，我们对初始数组采用随机化的方式)我们修该主函数

void inArr(int arr[],int length)
{
    for(int i=0;i<length;i++)
    {
        arr[i]=rand()%50;
    }
}
int main()
{
    srand((unsigned int)time(NULL));
    int arr[MAXSIZE];
    inArr(arr,MAXSIZE);
    showArr(arr,MAXSIZE);    //打印初始序列
    shell(arr,MAXSIZE);
    showArr(arr,MAXSIZE);    //打印排序后序列
    return 0;
}

这种初始数组的方式可以称为随机初始化

void shell(int arr[],int length)
{
    int h=length/2;
    while (h>=1)
    {
        for(int i=h;i<length;i++)
    {
        for(int j=i;j>=h && arr[j]<arr[j-h];j-=h)
        {
            int temp=arr[j];
            arr[j]=arr[j-h];
            arr[j-h]=temp;
        }
    }
    h/=2;
    }
}

希尔排序的效率完全取决于步长序列的选取，目前希尔排序的最优步长序列是“希尔序列” ；1，4，…,3n+1,所以经典的希尔排序如下:

void shell(int arr[],int length)
{
    int h=1;
    int t=length/3;
    while(h<t)
    {
        h=3*h+1;
    }
    while (h>=1)
    {
        for(int i=h;i<length;i++)
    {
        for(int j=i;j>=h && arr[j]<arr[j-h];j-=h)
        {
            int temp=arr[j];
            arr[j]=arr[j-h];
            arr[j-h]=temp;
        }
    }
    h/=3;
    }
}

(五)快速排序

冒泡排序的优化版本，核心思想：找到一个轴(pivot)，每一轮左右递归后，把轴放到中间，使得轴的左边都比轴小，轴的右边都比轴大。当所有的递归都结束了，也就排好序了。

void quickArr(int arr[],int left,int right)
{
    if(left>=right)
        return;
    int i=left;
    int j=right;
    int pivot=arr[i];
    while(i<j)
    {
        while(i<j && arr[j]>=pivot)
            j--;
        arr[i]=arr[j];
        while(i<j && arr[i]<=pivot)
            i++;
        arr[j]=arr[i];
    }
    arr[i]=pivot;          //循环结束后的新轴   i=j
    quickArr(arr,left,i-1);
    quickArr(arr,i+1,right);
}

考虑到数组只能进行顺序存储，故这个程序不能用于单向链表，我们对于单向链表提供如下思路：

void quicksort2(int arr[],int left,int right)
{
    if(left>=right)
            return;
    int pivot=arr[left];
    int i=left+1;
    int j=left+1;
    while(j<=right)
    {
        if(arr[j]<pivot)
        {
            int temp=arr[i];
            arr[i]=arr[j];
            arr[j]=temp;
            i++;
        }
        j++;
    }
    int temp=arr[i-1];
    arr[i-1]=pivot;
    pivot=temp;
    quicksort2(arr,left,i-2);
    quicksort2(arr,i,right);
}
// 这种方式专门针对单向链式存储

(六)归并排序

基于分而治之的思想。拿两个有序的序列重新组合成新的序列，

//arr和boy默认有序
void Mergesort(int arr[],int alen,int boy[],int blen,int *temp)
{
    int i=0;int j=0;int k=0;
    while(i<alen && j<blen)
        temp[k++]=arr[i]<boy[j] ? arr[i++]:boy[j++]; 
    while(i<alen)
        temp[k++]=arr[i++];
    while (j<blen)
        temp[k++]=boy[j++];
    
}

这是基础版排序

int main()
{
    int a[5]={1,3,5,7,9};
    int b[4]={2,4,6,8};
    int temp[9];
    Mergesort(a,5,b,4,temp);
    showArr(temp,9);
    return 0;
}

最终归并排序

void mergeg(int arr[],int low,int mid,int height,int *temp)
{
    int i=low;
    int j=mid+1;
    int k=low;
    while(i<=mid && j<=height)
        temp[k++]=arr[i]<arr[j] ? arr[i++]:arr[j++];
    while(i<=mid)
        temp[k++]=arr[i++];
    while(j<=height)
        temp[k++]=arr[j++];
    for(i=low;i<=height;i++)
        arr[i]=temp[i];
}
void mergeg_sort(int arr[],int low,int height,int *temp)
{
    if(low>=height)
        return;
    int mid=low+(height-low)/2;
    //若用 mid=(height+low)/2可能会越界
    mergeg_sort(arr,low,mid,temp);
    mergeg_sort(arr,mid+1,height,temp);
    mergeg(arr,low,mid,height,temp);
}
void mergegSort(int arr[],int length)
{
    int *temp=(int*)malloc(sizeof(int)*length);
    assert(temp);
    mergeg_sort(arr,0,length-1,temp);
    free(temp);
}

(七)计数排序

算法思想:统计原来数组的数据,并将数据转换成为下标储存于一个临时空间中，然后遍历临时空间，把对应下标值放回原来数组。当遍历结束后，原数组就排好序了。

#define N 100
int temp[N];//全局变量自动初值为零
void countSort(int arr[],int length)
{
    for(int i=0;i<length;i++)
        temp[arr[i]]++;
    for(int i=0,j=0;i<N;i++)
        while(temp[i]--)
            arr[j++]=i; 
}

(八)基数排序

对每位数上的数字用计数排序，与计数排序类似都是基于桶排序
例如:
234 456 121 223 416

第一轮($ 10^0 $位上):121 223 234 456 416

第二轮($ 10^1 $位上):416 121 223 234 456

第三轮($ 10^2 $位上):121 223 234 416 456

int Temp[10][MAXSIZE];
void redixSort(int arr[],int length)
{
    int i,j,pos,k;
    for(k=10;k<1000;k*=10)
    {
        for(i=0;i<length;i++)
        {
            j=0;
            pos=(arr[i]%k)/(k/10);
            while(Temp[pos][j])
                j++;
            Temp[pos][j]=arr[i];
        }
        pos=0;
        for(i=0;i<10;i++)
        {
            for(j=0;j<length && Temp[i][j] !=0;j++)
            {
                arr[pos++]=Temp[i][j];
                Temp[i][j]=0;
            }
        }
    }
}